El uso de datos relacionales en las ciencias sociales ha aumentado en las últimas dos décadas, impulsado por el interés en las estructuras de redes y sus implicaciones conductuales. Sin embargo, los métodos para analizar dichos datos no están desarrollados, lo que conduce a investigaciones ad hoc e invariables y dificulta el desarrollo de teorías sólidas. Dos métodos emergentes, los modelos de bloques y los modelos estocásticos para dígrafos, ofrecen soluciones prometedoras. Los modelos de bloques describen claramente la estructura y los roles globales, pero carecen de modelos claros de variabilidad de datos y pruebas formales de ajuste. Por otro lado, los modelos estocásticos manejan la variabilidad de los datos y las pruebas de ajuste, pero no modelan la estructura global ni las relaciones. La combinación de estos métodos puede abordar sus limitaciones y mejorar el análisis de datos relacionales.
Los investigadores del Educational Testing Service y de la Universidad Carnegie-Mellon propusieron un modelo estocástico para redes sociales, que divide a los actores en subgrupos llamados bloques. Este modelo amplía los modelos de bloques tradicionales incorporando elementos estocásticos y métodos de estimación para una red relacional con bloques predefinidos. También introduce una extensión para tener en cuenta las probabilidades recíprocas vinculadas, que proporciona una prueba de un grado de libertad para el ajuste del modelo. El estudio analiza la integración de este método con multigrafos estocásticos y modelos de bloques, describe pruebas de ajuste formales y utiliza un ejemplo numérico de la literatura sobre redes sociales para ilustrar los métodos. La conclusión relaciona los modelos de bloques estocásticos con otros tipos de modelos de bloques.
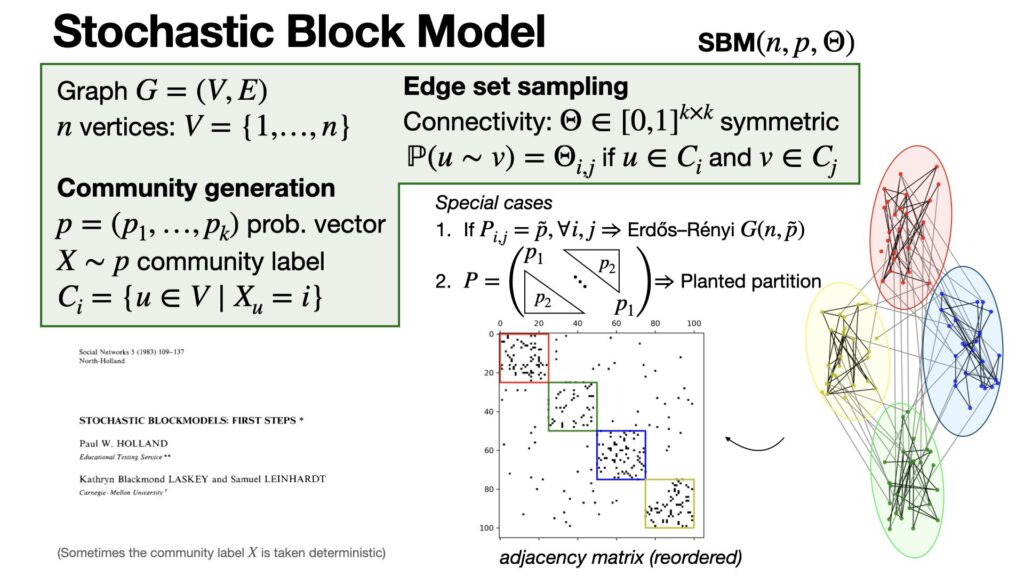
Un modelo de bloques estocástico es un marco utilizado para analizar datos sociométricos donde una red se divide en subgrupos o bloques, y la distribución de las relaciones entre nodos depende de estos bloques. Este modelo formaliza el modelo de bloques determinista introduciendo variabilidad de datos. Este es un tipo específico de distribución de probabilidad de matrices de adyacencia, donde los nodos se dividen en bloques y los enlaces entre nodos dentro del mismo bloque se modelan como estadísticamente equivalentes. El modelo supone que las relaciones entre nodos en el mismo bloque se distribuyen por igual e independientemente de las relaciones entre otros pares de nodos, formalizando el concepto de “homogeneidad interna” dentro de los bloques.
En aplicaciones prácticas, los modelos de bloques estocásticos analizan datos sociométricos relacionales con bloques predefinidos. El modelo facilita la estimación, centrándose en las densidades de bloques, de la probabilidad de un vínculo entre nodos en bloques específicos. El proceso de estimación implica calcular la función de verosimilitud de los datos observados y obtener la estimación de máxima verosimilitud para la densidad de bloques. Este método es particularmente eficiente porque la función de verosimilitud es rastreable y la estimación de máxima verosimilitud se puede calcular directamente a partir de las densidades de bloques observadas. Este enfoque permite el cálculo de medidas como relaciones recíprocas, proporcionando información sobre la estructura de la red más allá de lo que pueden hacer los modelos deterministas.
El estudio explora técnicas avanzadas de modelado de bloques para analizar la reciprocidad y las estructuras a nivel de pareja en las redes sociales. Analiza el concepto de reciprocidad, donde la mutualidad de las relaciones puede exceder las expectativas aleatorias, e introduce el modelo de bloques estocástico dependiente de pares (PSB), que tiene en cuenta las dependencias entre relaciones. El modelo de bloques estocástico con reciprocidad (SBR) es un caso específico de PSB que incluye parámetros para vínculos mutuos, asimétricos y nulos. El texto también incluye estimaciones utilizando la estimación de máxima verosimilitud (MLE) y pruebas de ajuste de modelos. Un ejemplo empírico de los datos del Monasterio Sampson ilustra la aplicación práctica de estos modelos.
En conclusión, el extracto analiza dos temas importantes relacionados con los modelos de bloques no estocásticos. Primero, aborda el desafío del cierre, señalando que los modelos de bloques estocásticos no están cerrados bajo el producto binario de matrices de adyacencia, lo que complica la comprensión de las relaciones indirectas. En segundo lugar, examina el enfoque bayesiano para generar bloques, donde los bloques no se determinan de antemano sino que se descubren a partir de los datos. Este método determina la cantidad de bloques, las distribuciones de tamaño de bloques y los parámetros de densidad para diferentes tipos de bloques. El modelo bayesiano permite la estimación de la probabilidad posterior de las membresías de bloques, lo que ayuda a un análisis de datos relacionales más sistemático.
Ver el ROLE. Todo el crédito por esta investigación va a los investigadores de este proyecto. Además, no olvides seguirnos en Gorjeo y únete a nosotros canal de telegramas y LinkedIn Grups. Si te gusta nuestro trabajo, te encantará nuestro trabajo. hoja informativa..
No olvides unirte a nuestro SubReddit de más de 50.000 ml
A Sana Hassan, pasante de consultoría en Marktechpost y estudiante de doble titulación en IIT Madras, le apasiona el uso de la tecnología y la inteligencia artificial para abordar los desafíos del mundo real. Con un gran interés en resolver problemas prácticos, aporta una nueva perspectiva a la intersección de la IA y las soluciones de la vida real.
